How To Draw A Snake And Ladder

Given a snake and ladder board, find the minimum number of dice throws required to reach the destination or last cell from source or 1st cell. Basically, the player has total control over outcome of dice throw and wants to find out minimum number of throws required to reach last cell.
If the player reaches a cell which is base of a ladder, the player has to climb up that ladder and if reaches a cell is mouth of the snake, has to go down to the tail of snake without a dice throw.

snakesandladders

Become a success story instead of just reading about them. Prepare for coding interviews at Amazon and other top product-based companies with our Amazon Test Series. Includes topic-wise practice questions on all important DSA topics along with 10 practice contests of 2 hours each. Designed by industry experts that will surely help you practice and sharpen your programming skills. Wait no more, start your preparation today!

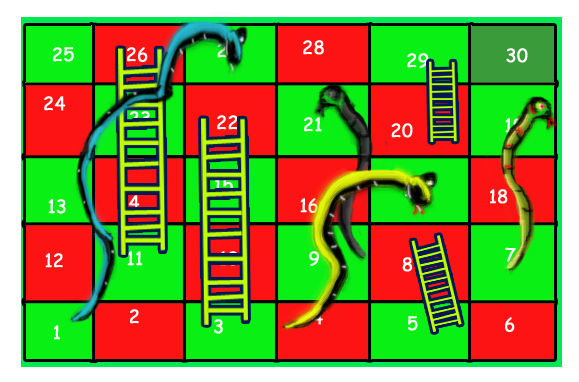
For example, consider the board shown, the minimum number of dice throws required to reach cell 30 from cell 1 is 3.
Following are the steps:
a) First throw two on dice to reach cell number 3 and then ladder to reach 22
b) Then throw 6 to reach 28.
c) Finally through 2 to reach 30.
There can be other solutions as well like (2, 2, 6), (2, 4, 4), (2, 3, 5).. etc.

The idea is to consider the given snake and ladder board as a directed graph with number of vertices equal to the number of cells in the board. The problem reduces to finding the shortest path in a graph. Every vertex of the graph has an edge to next six vertices if next 6 vertices do not have a snake or ladder. If any of the next six vertices has a snake or ladder, then the edge from current vertex goes to the top of the ladder or tail of the snake. Since all edges are of equal weight, we can efficiently find shortest path using Breadth First Search of the graph.
Following is the implementation of the above idea. The input is represented by two things, first is 'N' which is number of cells in the given board, second is an array 'move[0…N-1]' of size N. An entry move[i] is -1 if there is no snake and no ladder from i, otherwise move[i] contains index of destination cell for the snake or the ladder at i.

C++

#include<iostream>

#include <queue>

using namespace std;

struct queueEntry

{

int v;

int dist;

};

int getMinDiceThrows( int move[], int N)

{

bool *visited = new bool [N];

for ( int i = 0; i < N; i++)

visited[i] = false ;

queue<queueEntry> q;

visited[0] = true ;

queueEntry s = {0, 0};

q.push(s);

queueEntry qe;

while (!q.empty())

{

qe = q.front();

int v = qe.v;

if (v == N-1)

break ;

q.pop();

for ( int j=v+1; j<=(v+6) && j<N; ++j)

{

if (!visited[j])

{

queueEntry a;

a.dist = (qe.dist + 1);

visited[j] = true ;

if (move[j] != -1)

a.v = move[j];

else

a.v = j;

q.push(a);

}

return qe.dist;

}

int main()

{

int N = 30;

int moves[N];

for ( int i = 0; i<N; i++)

moves[i] = -1;

moves[2] = 21;

moves[4] = 7;

moves[10] = 25;

moves[19] = 28;

moves[26] = 0;

moves[20] = 8;

moves[16] = 3;

moves[18] = 6;

cout << "Min Dice throws required is " << getMinDiceThrows(moves, N);

return 0;

}

Java

import java.util.LinkedList;

import java.util.Queue;

public class SnakesLadder

{

static class qentry

{

int v;

int dist;

}

static int getMinDiceThrows( int move[], int n)

{

int visited[] = new int [n];

Queue<qentry> q = new LinkedList<>();

qentry qe = new qentry();

qe.v = 0 ;

qe.dist = 0 ;

visited[ 0 ] = 1 ;

q.add(qe);

while (!q.isEmpty())

{

qe = q.remove();

int v = qe.v;

if (v == n - 1 )

break ;

for ( int j = v + 1 ; j <= (v + 6 ) && j < n; ++j)

{

if (visited[j] == 0 )

{

qentry a = new qentry();

a.dist = (qe.dist + 1 );

visited[j] = 1 ;

if (move[j] != - 1 )

a.v = move[j];

else

a.v = j;

q.add(a);

}

return qe.dist;

}

public static void main(String[] args)

{

int N = 30 ;

int moves[] = new int [N];

for ( int i = 0 ; i < N; i++)

moves[i] = - 1 ;

moves[ 2 ] = 21 ;

moves[ 4 ] = 7 ;

moves[ 10 ] = 25 ;

moves[ 19 ] = 28 ;

moves[ 26 ] = 0 ;

moves[ 20 ] = 8 ;

moves[ 16 ] = 3 ;

moves[ 18 ] = 6 ;

System.out.println( "Min Dice throws required is " +

getMinDiceThrows(moves, N));

}

Python3

class QueueEntry( object ):

def __init__( self , v = 0 , dist = 0 ):

self .v = v

self .dist = dist

def getMinDiceThrows(move, N):

visited = [ False ] * N

queue = []

visited[ 0 ] = True

queue.append(QueueEntry( 0 , 0 ))

qe = QueueEntry()

while queue:

qe = queue.pop( 0 )

v = qe.v

if v = = N - 1 :

break

j = v + 1

while j < = v + 6 and j < N:

if visited[j] is False :

a = QueueEntry()

a.dist = qe.dist + 1

visited[j] = True

a.v = move[j] if move[j] ! = - 1 else j

queue.append(a)

j + = 1

return qe.dist

N = 30

moves = [ - 1 ] * N

moves[ 2 ] = 21

moves[ 4 ] = 7

moves[ 10 ] = 25

moves[ 19 ] = 28

moves[ 26 ] = 0

moves[ 20 ] = 8

moves[ 16 ] = 3

moves[ 18 ] = 6

print ( "Min Dice throws required is {0}" .

format (getMinDiceThrows(moves, N)))

C#

using System;

using System.Collections.Generic;

public class SnakesLadder

{

public class qentry

{

public int v;

public int dist;

}

static int getMinDiceThrows( int []move, int n)

{

int []visited = new int [n];

Queue<qentry> q = new Queue<qentry>();

qentry qe = new qentry();

qe.v = 0;

qe.dist = 0;

visited[0] = 1;

q.Enqueue(qe);

while (q.Count != 0)

{

qe = q.Dequeue();

int v = qe.v;

if (v == n - 1)

break ;

for ( int j = v + 1; j <= (v + 6) && j < n; ++j)

{

if (visited[j] == 0)

{

qentry a = new qentry();

a.dist = (qe.dist + 1);

visited[j] = 1;

if (move[j] != -1)

a.v = move[j];

else

a.v = j;

q.Enqueue(a);

}

return qe.dist;

}

public static void Main(String[] args)

{

int N = 30;

int []moves = new int [N];

for ( int i = 0; i < N; i++)

moves[i] = -1;

moves[2] = 21;

moves[4] = 7;

moves[10] = 25;

moves[19] = 28;

moves[26] = 0;

moves[20] = 8;

moves[16] = 3;

moves[18] = 6;

Console.WriteLine( "Min Dice throws required is " +

getMinDiceThrows(moves, N));

}

Javascript

<script>

class qentry

{

constructor()

{

this .v = 0;

this .dist = 0;

}

function getMinDiceThrows(move,n)

{

let visited = new Array(n);

for (let i = 0; i < n; i++)

visited[i] = false ;

let q = [];

let qe = new qentry();

qe.v = 0;

qe.dist = 0;

visited[0] = 1;

q.push(qe);

while (q.length != 0)

{

qe = q.shift();

let v = qe.v;

if (v == n - 1)

break ;

for (let j = v + 1; j <= (v + 6) && j < n; ++j)

{

if (visited[j] == 0)

{

let a = new qentry();

a.dist = (qe.dist + 1);

visited[j] = 1;

if (move[j] != -1)

a.v = move[j];

else

a.v = j;

q.push(a);

}

return qe.dist;

}

let N = 30;

let moves = new Array(N);

for (let i = 0; i < N; i++)

moves[i] = -1;

moves[2] = 21;

moves[4] = 7;

moves[10] = 25;

moves[19] = 28;

moves[26] = 0;

moves[20] = 8;

moves[16] = 3;

moves[18] = 6;

document.write( "Min Dice throws required is " +

getMinDiceThrows(moves, N));

</script>

Output:

Min Dice throws required is 3

Time complexity of the above solution is O(N) as every cell is added and removed only once from queue. And a typical enqueue or dequeue operation takes O(1) time.

This article is contributed by Siddharth. Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.